Effect of Harmonic Components on EMF of Alternators:
Before knowing Effect of Harmonic Components on EMF let us know what are harmonics and harmonic components in alternators. In synchronous machines, voltages and currents are induced, which are in sinusoidal waveforms. But in practice, these sinusoidal waveforms will deviate to form non-sinusoidal waveforms.
These non-sinusoidal waveforms are expressed in terms of Fourier transforms which are the sum of series of sinusoidal waveforms. Now let us understand the effect of harmonic components on the synchronous generator.
Must Read:
- Principle and working of Synchronous generator or alternator
- Harmonics in Synchronous Machines(Alternators) | Slot Harmonics
The flux density distribution around the air gap in all well designed alternators symmetrical with respect to the abscissa and also to polar axes.Thus it can be expressed with the help of a Fourier series which do not contain any even harmonics.
So flux density at any angle θ from the interpolar axis is given by,
B = Bm1 sin θ + Bm3 sin 3θ +……….. + Bmx sin xθ
where x = Order of the harmonic component which is odd
Bm1 = Amplitude of fundamental component of flux density
Bm3 = Amplitude of 3rd harmonic component of flux density
Bmx = Amplitude of Xth (odd) harmonic component of flux density
The EMF generated in a conductor on the armature of a rotating machine is given by
ec = B.l.v
Substituting value of B,
ec = [Bm1 sin θ + Bm3 sin 3θ +……….. + Bmx sin xθ].l.v
l = Active length of conductor in metre
d = Diameter of the armature at the air gap
v = Linear velocity = π d ns
where ns = Synchronous speed in r.p.s.
Now NS = 120f/P
ns = 120f/60P = 2f/P
v = π d 2f/P
Substituting in the expression for ec ,
ec = [Bm1 sin θ + Bm3 sin 3θ +……….. + Bmx sin xθ].l.(2πdf/P)
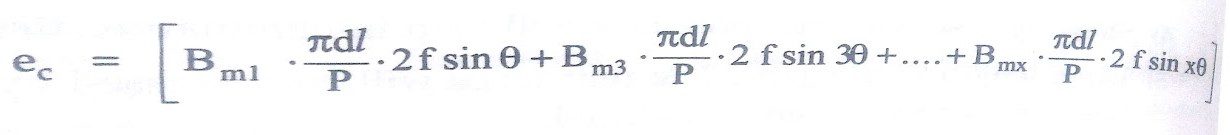
Area of each fundamental pole,
A1 = πdl/P
ec = [Bm1 A1 2f sin θ + Bm3 A1 2f sin 3θ +……….. + Bmx A1 2f sin xθ]
Area of xth harmonic pole, Ax = πdl/xP = A1/x
This is because there are xP poles for the xth order harmonic.
ec = 2f [Bm1 A1 sin θ + Bm3 3A3 sin 3θ +……….. + Bmx xAx sin xθ]
Bm1 A1 = Φ1m = Maximum value of fundamental flux per pole
Φ1= (2/π)Φ1m = Average value of fundamental flux per pole
Similarly, the average value of xth harmonic flux per pole can be obtained as,
Φx = (2/π)Ax Bmx
Substituting the values of flux in ec we get the expression for e.m.f. induced per conductor as
ec = πf (Φ1 sin θ + 3Φ3 sin 3θ +……….. + xΦx sin xθ)
Instantaneous value of fundamental frequency EMF generated in a conductor is,
ec1 = πfΦ1 sin θ V
Hence the R.M.S. value of fundamental frequency EMF generated in a conductor is,
ec1 = πfΦ1/√2 = 2.22 fΦ1
Hence RMS value ofxthharmonic frequency emf generated in a conductor is,
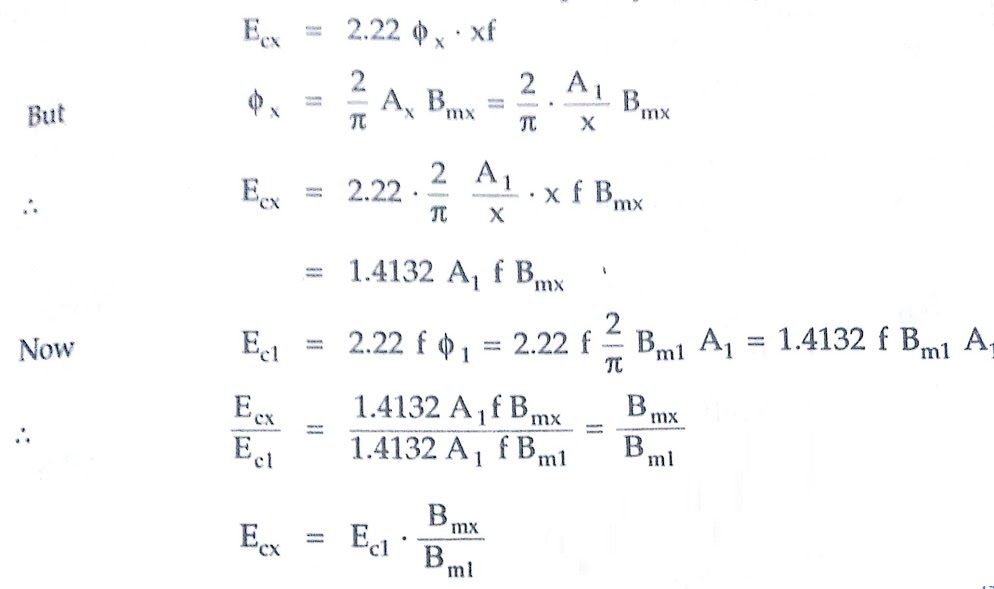
It can be observed that the magnitude of harmonic e.m.f.s are directly proportional to their corresponding flux densities.
The RMS value of resultant EMF of a conductor is,
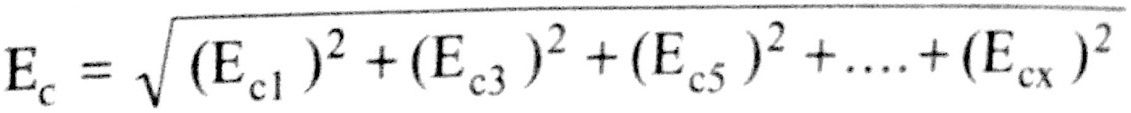
Effect of Harmonic Components on Pitch Factor in Synchronous Generator:
We know that,
α = Angle of the short pitch for fundamental flux wave then it changes for the various harmonic component of flux as,
3α = For 3rd harmonic component
5α = For 5th harmonic component
xα = For xth harmonic component
Hence the pitch factor is expressed as,
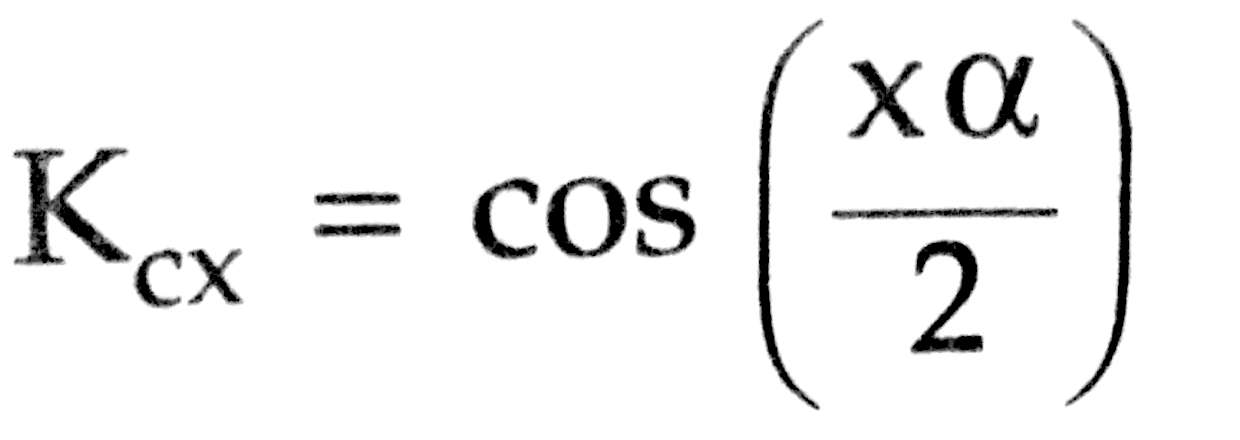
x = Order of the harmonic component
Effect of Harmonic Components on Distribution Factor in Alternators:
Similar to the pitch factor, the distribution factor is also different for various halt components.
The general expression to obtain distribution factor is,

Total EMF Generated due to Harmonics in synchronous Generator:
Consider the windings to short pitch and distributed, the e.m.f. of a fundamental frequency is given by,
E1ph = 4.44 Kc1 Kd1 Φ1 f Tph V
where Tph = Turns per phase in series
Φ1 = Fundamental flux component
While the phase e.m.f. of Xth order harmonic component of frequency is given by,
Exph = 4.44 Kcx Kdx Φx (xf) Tph V
The total phase EMF is given by,
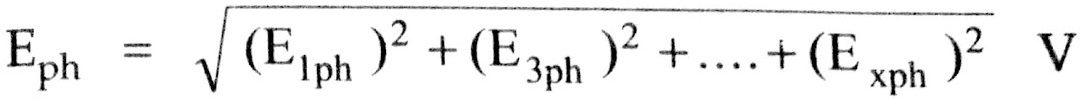
Line EMF: For star connected, the line or terminal induced EMF is √3 times the total phase EMF.But it should be noted that with star connection, the 3rd harmonic voltages do not appear across line terminals though present in phase voltage.
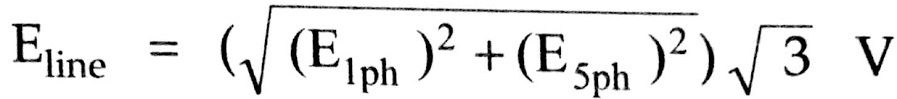
Key Point: In delta connection also, 3rd,9th,15th….. harmonic voltages do not appear at the line terminals.
Must Read:
Taking ratio of fundamental frequency EMF and Xth order harmonic frequency EMF we can write,
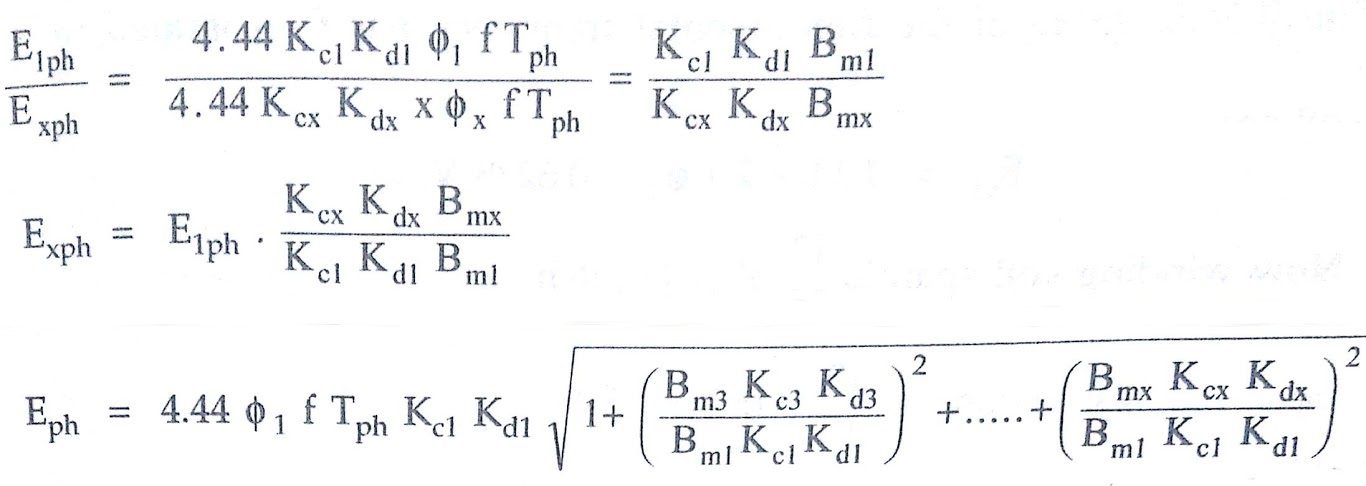
From the ratio in above equation, we can write
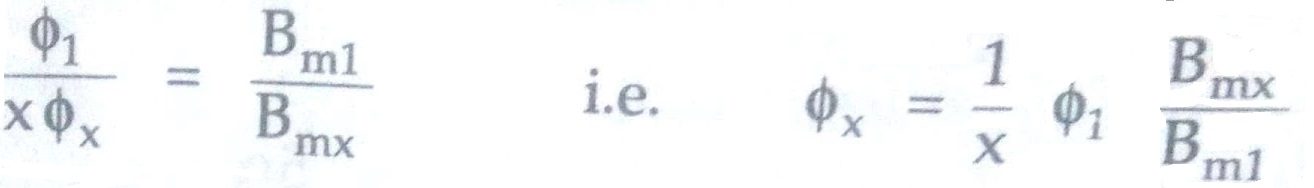
Thus if the third harmonic is given to be 10% of fundamental
Φ3 = 1/3*(10% of Φ1) = 0.0333Φ1
Conclusion:
Now today we have learnt about Effect of Harmonic Components on Synchronous Generator or Alternator and also emf generated due to harmonic components in Synchronous Generator or Alternator.You can download this article as pdf, ppt.
Comment below for any Queries.
