Transfer function of Thermal System:
Let us derive the formula for transfer function of thermal system and mathematical model of thermal System:
List of symbols used in thermal system.
q = Heat flow rate, Kcal/sec.
θ1 = Absolute temperature of emitter, °K.
θ2 = Absolute temperature of receiver, °K.
∆θ = Temperature difference, °C.
A = Area normal to heat flow, m²
K = Conduction or Convection coefficient; Kcal/sec-°C.
Kr = Radiation coefficient, Kcal/sec-°C.
H = K/A=Convection coefficient, Kcal/m2-sec-°C.
H = Thermal conductivity , K cal/m-sec-°C.
∆X = Thickness of conductor,m
R = Thermal resistance, °C-sec/Kcal
C = Thermal capacitance, Kcal/°C
Heat Flow Rate:
Thermal systems are those that involve the transfer of heat from one substance to another. There are three difference ways of heat flow from one substance to another. They are conduction, convection and radiation.
For conduction,
Heat flow rate = q = K ∆θ = KA/∆X
For convection,
Heat flow rate, q= K ∆θ = HA ∆θ
For radiation,
Heat flow rate, q = Kr(θ1⁴ – θ2⁴)
If θ1 » θ2 then, q = Kr θ⁴
Where θ4 = (θ1⁴ – θ2⁴)¹/⁴
Note : θ4 is called effective temperature difference of the emitter and receiver.
Mathematical model of thermal system:
The model of thermal systems are obtained by using thermal resistance and capacitance which are the basic elements of the thermal system. The thermal resistance and capacitance are distributed in nature. But for simplicity in analysis lumped parameter models are used.
In lumped parameter model it is assumed that the substances that are characterized by resistance to heat flow have negligible heat capacitance and the substances that are characterized by heat capacitance have negligible resistance to heat flow. The thermal resistance, R for heat transfer between two substances is defined as the ratio of change in temperature and change in heat flow rate.
The thermal resistance, R for heat transfer between two substances is defined as the ratio of change in temperature and change in heat flow rate.
For conduction or convection,
Heat flow rate, q = K ∆θ
On differentiating we get,
dq = K d(∆θ)
d(∆θ)/dq = 1/K
But thermal resistance, R = d(∆θ)/dq
Thermal resistance, R = 1/K for conduction
= 1/K = 1/HA = for convection
For radiation,
Heat flow rate, q = Krθ⁴
On differentiating we get
dq = Kr 4 θ³ dθ
dθ/dq = 1/Kr4 θ³
But thermal resistance, R = dθ/dq
Thermal resistance, R = 1/4Kr θ³ (for radiation)
Thermal Capacitance, C is defined as the ratio of change in heat stored and change in temperature.
Let M = Mass of substance considered, Kg
c = Specific heat of substance, Kcal/Kg -°C
Now, Thermal capacitance, C = Mcp
Transfer function of Thermal system:
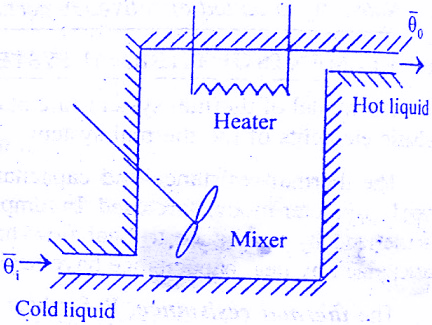
Consider a simple thermal system shown in the below figure. Let us assume that the tank is insulated to eliminate heat loss to the surrounding air, there is no heat storage in the insulation and liquid in the tank is kept at uniform temperature by perfect mixing with the help of a stirrer. Thus, a single temperature is used to describe the temperature of the liquid in the tank and of the out flowing liquid. The transfer function of thermal system can be derived as shown below.
Let θ1 = Steady state temperature of inflowing liquid, °C
θ0 = Sandy state temperature of outflowing liquid, °C
G = Steady state liquid flow rate, Kg/sec
M = Mass of liquid in tank, Kg
c = Specific heat of liquid, Kcal/Kg °C
R = Thermal resistance, °C – sec/Kcal
C = Thermal capacitance, Kcal/°C
Q = Steady state heat input rate, Kcal/Sec
Let us assume that the temperature of inflowing liquid is kept constant. Let the heat input rate to the thermal system supplied by the heater is suddenly changed from Q to Q + q1.Due to this, the heat output flow rate will gradually change from Q to Q + q0.The temperature of the outflowing liquid will also be changed from θ0 to θ0 + θ.
For this system the equation for q0, C and R are obtained as follows,
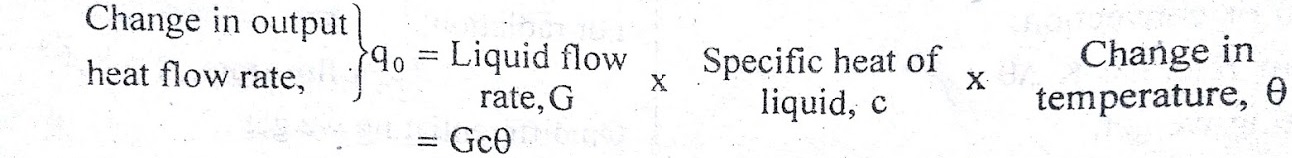
Thermal capacitance, C = Mass, M x Specific heat of liquid, c = Mc
On substituting for qo from equation (1) in equation (3) we get,
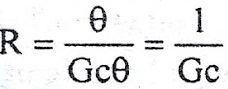
In this thermal system, rate of change of temperature is directly proportional to change in heat input rate.
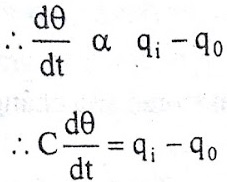
The constant of proportionality is capacitance C of the system.
Equation (5) is the differential equation governing system.Since equation (5) is of first order equation, the system is first order system.
From equation (3) , R = θ/q0
q0 = θ/R
On substituting for q0 from equation (6) in equation (5) we get,
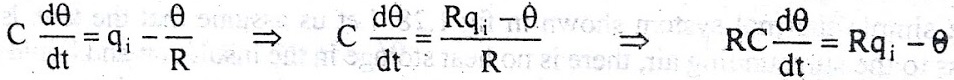
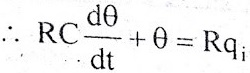
Let, L {θ} = θ(s); L{dθ/dt} = sθ(s) ; L{q1} = Q1(s)
On taking Laplace transform of equation (7)
RC s θ(s) + θ(s) = R Q1(s)
θ(s) [sRC + 1] = R Q1(s)
θ(s)/Q1(s) is the required transfer function of thermal system.
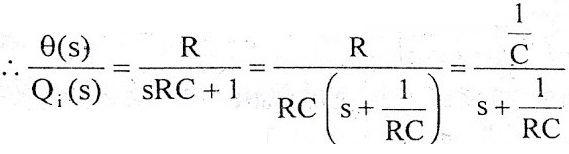
Advantages of Using Transfer Functions:
Transfer functions offer several advantages when modeling thermal systems:
- Simplicity: Transfer functions provide a concise representation of complex systems, making it easier to analyze and understand their behavior.
- Frequency Analysis: Transfer functions allow frequency-domain analysis, enabling engineers to predict system response to different input frequencies and design filters or controllers accordingly.
- Control System Design: Transfer functions play a crucial role in designing control systems. They help in tuning controller parameters for desired performance and stability.
- Model Validation: Transfer function models can be validated against real-world data, allowing engineers to fine-tune the model and improve accuracy.
- Simulation: Transfer functions can be used in simulation software to predict system behavior under various conditions before implementing changes in the real system.
Conclusion:
In this post we have learnt transfer function and mathematical Model of thermal system.You can download this article as pdf,ppt.
Comment below if you have any queries!
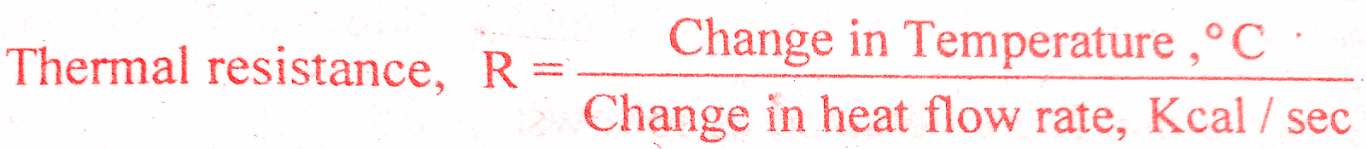
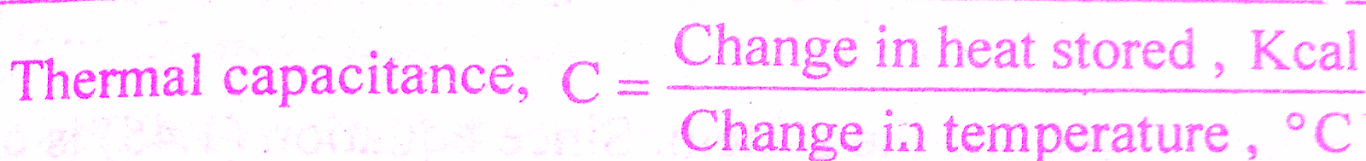
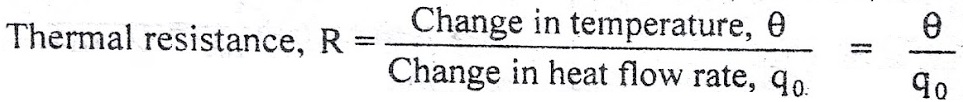
Excellent material