Blondel Two Reaction Theory:
We knew that in non-salient pole type alternators the air gap is uniform. Due to the uniform air gap, the field flux, as well as armature flux vary sinusoidally in the air gap. In nonsalient pole alternators, air gap length is constant and reactance is also constant. This two reaction theory was given by Professor Andre Blondel so it is named as Blondel two reaction theory.
Due to this, the MMFs of armature and field act upon the same magnetic circuit all the time hence can be added vectorially. But in salient pole type alternators, the length of the air gap varies and the reluctance also varies. Hence the armature flux and field flux cannot vary sinusoidally in the air gap. The reluctances of the magnetic circuits on which MMFs act are different in the case of salient pole alternators.
Hence the armature and field MMF’s are given special importance while given less importance in a nonsalient pole alternators. There are some disturbing factors in salient pole alternators which are analysed below. The theory which gives the method of analysis of the disturbing effects caused by salient pole construction is called Two Reaction Theory.
Must Read:
Key Point: According to this theory, the armature m.m.f. can be divided into two components as,
1. Component acting along the pole axis called direct axis.
2. Component acting at right angles to the pole axis called quadrature axis.
The component which is acting along the direct axis can be magnetising or demagnetising.The component which is acting along quadrature axis is cross magnetising.These components produce the effects of different kinds.The below figure shows the stator MMF wave and the flux distribution in the airgap along direct axis and quadrature axis of the pole.
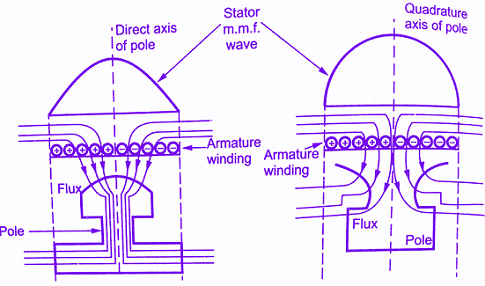
The reluctance offered to the MMF wave is lowest when it is aligned with the field pole axis.This axis is called the direct axis of pole i.e. d-axis.The reluctance offered is highest when the MMF wave is oriented at 90° to the field pole axis which is called quadrature axis i.e. q-axis.
The air gap is least in the centre of the poles and progressively increase, on moving away from the centre.Due to such shape of the pole-shoes, the field winding wound on salient poles produces the MMF wave which is nearly sinusoidal and it always acts along the pole axis which is direct axis.
Let Ff be the MMF wave produced by field winding, then it always acts along the direct axis. This MMF is responsible for producing an excitation EMF Ef which lags Ff by all angle 90°.
When armature carries current, it produces its own MMF wave FAR. This can be resolved into two components, one acting along d-axis (magnetising or demagnetising) and one acting along q-axis (cross-magnetising). Similarly, armature current Ia also can in divided into two components, one along the direct axis and one along quadrature axis. These components are denoted as,
FAR :
Fd = component along direct axis
Fq = component along quadrature axis
Ia :
Id = component along direct axis
Iq = component along quadrature axis
The positions of FAR, Fd and Fq in space are shown in the below figure. The instant chosen to show these positions is such that the current in phase R is maximum positive and is lagging Ef by angle Ψ.
The phasor diagram of MMF wave positions in salient pole machine is shown below.
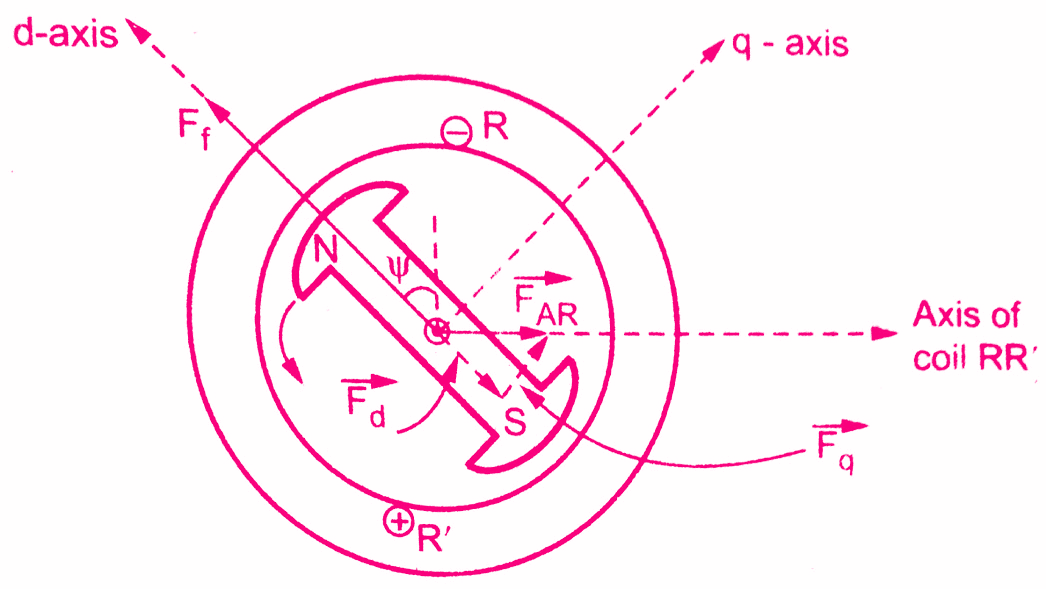
It can be observed from the figure that Fd is produced by Id which is at 90° to Ef while Fq is produced by Iq which is in phase with Ef.The flux components of ΦAR which are Φd and Φq respectively are also shown in the below figure.
It can be noted that the reactance offered to flux along the direct axis is less than the reactance offered to flux along quadrature axis.Due to this, the flux ΦAR is no longer along FAR or Ia.Depending upon the reluctances offered along the direct and quadrature axis, the flux ΦAR lags behind armature current Ia.
Direct and Quadrature Axis Synchronous Reactances:
We already know that the armature reaction flux ΦAR has two components, one is Φd along the direct axis and Φq along quadrature axis. These fluxes are proportional to the respective MMF magnitudes and the permeance of the flux path oriented along the respective axes.Here below were are going to derive the terminal voltage in Blondel two reaction theory.
Φd = Pd Fd
where Pd = Permeance along the direct axis
Permeance is the reciprocal of reluctance and indicates ease with which flux can travel along the path.
But Fd = M.M.F. = Kar Id in phase with Id
The MMF is always proportional to current.While Kar is the armature reaction coefficient.
∴ Φd = Pd Kar Id
Similarly Φq = Pq Kar Iq
As the reluctance along the direct axis is less than that along quadrature axis, permeance Pd along direct axis is more than that along quadrature axis, (Pd > Pq).
Let Ed and Eq be the induced e.m.f.s due to the fluxes Φd and Φq respectively.
Now Ed lags Φd by 90° while Eq lags Φq by 90°.
∴ Ed = Ke Φd ∠-90° = — j Ke Φd
and Eq = Ke Φq ∠-90° = — j Ke Φq
where Ke = e.m.f. constant of armature winding.
The resultant e.m.f. is the phasor sum of Ef, Ed and Eq.
ER = Kf + Ed + Eq
= Ef – j Ke Φd – jKe Φq
Substituting expressions for Φd and Φq
ER = Ef – j Ke Pd Kar Id – j Ke Pq Kar Iq
where Xard = Equivalent reactance corresponding to the d-axis component of armature reaction
= Ke Pd Kar
Xarq = Equivalent reactance corresponding to the q-axis component of armature reaction
= Ke Pq Kar
ER = Ef — j Xard Id — Xarq Iq
where Vt = Terminal voltage
XL = Leakage reactance
But Ia = Id +Iq
Vt + Ia Ra + XL Id + XL Iq
Substituting in expression for ER,
Vt + Ia Ra + XL Id + XL Iq = Ef—j Xard Id—j Xarq Iq
Ef = Vt + Ia Ra + j (XL + Xard) Id + (XL + Xarq) Iq
Ef = Vt + Ia Ra + j Xd Id + j Xq Iq
where Xd = d-axis synchronous reactance = Xd + Xard
Xq = q-axis synchronous reactance = XL + Xarq
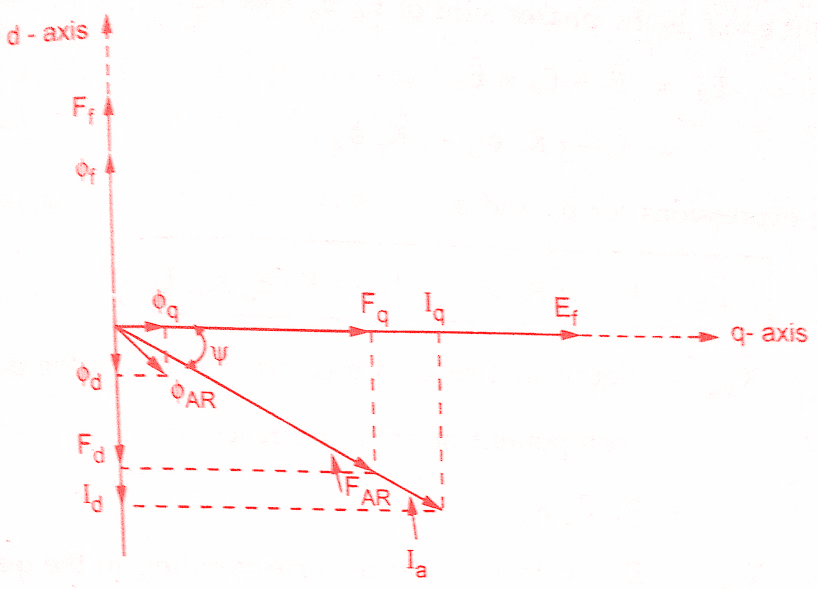
From the above equation we can observe that the terminal voltage Vt is nothing but the voltage left after deducting ohmic drop Ia Ra, the reactive drop Id Xd in quadrature with Id and the reactive drop lqXq in quadrature with Iq from the total EMF Ef.The Blondel two reaction theory phasor diagram corresponding to the first equation is shown as in the figure below.
The current Ia lags terminal voltage Vt by Φ.Then add Ia Ra in phase with la to Vt.The drop Id Xd leads Id by 90° as in case purely reactive circuit current lags voltage by 90° i.e. voltage leads current by 90°.Similarly, the drop IqXq leads Xq by 90°.The total EMF is Ef.
Blondel two reaction theory phasor diagram Analysis :
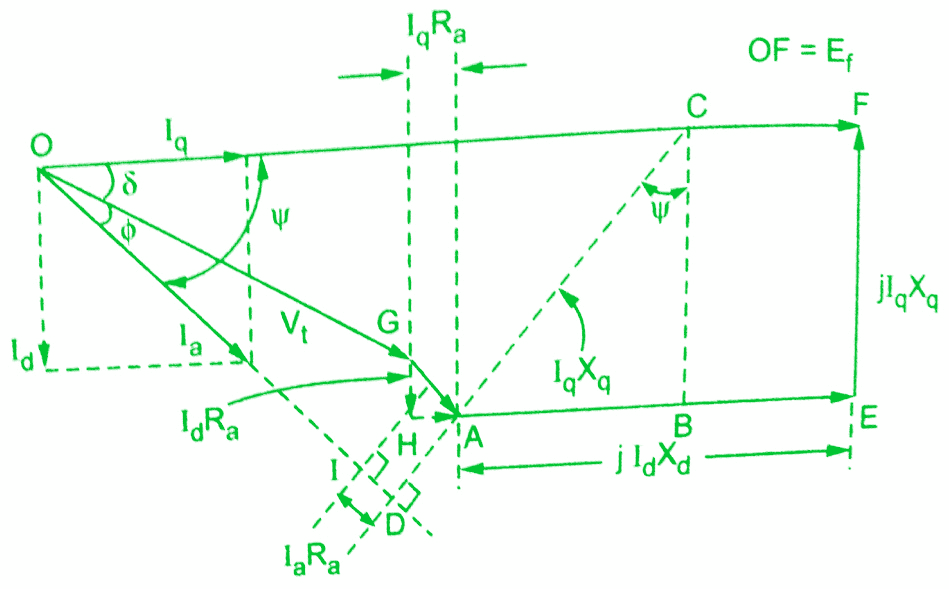
From the Blondel two reaction theory phasor diagram shown in the below figure, the angles Ψ and 𝛿 values are unknown, though Vt, Ia and Φ values are known.Hence the location of Ef is also unknown.The components of Ia, Id and Iq can not be determined which are required to sketch the phasor diagram.Let us find out some geometrical relationships between the various quantities which are involved in the phasor diagram.
 |
| Blondel two reaction theory phasor diagram |
To understand this,Blondel two reaction theory phasor diagram is drawn as shown above.
From phasor diagram
Id = Ia Sin Ψ
Iq = Ia Cos Ψ
Cos Ψ = Iq/Ia
The drop IaRa has two components.They are
IdRd = drop due to Ra in phase with Id
IqRa = drop due to Ra in phase with Iq
The IdXd and IqXq can be drawn leading Id and Iq by 90° respectively.The detailed Blondel two reaction theory phasor diagram for lagging power factor is shown below.
In the phasor diagram,
OF = Ef
OG = Vt
GH = Id Ra and HA = Iq Ra
GA = Ia Ra
AE = Id Xd and EF = Iq Xq
Now DAC is drawn perpendicular to the current phasor Ia and CB is drawn perpendicular to AE.
The triangle ABC is right angled triangle.
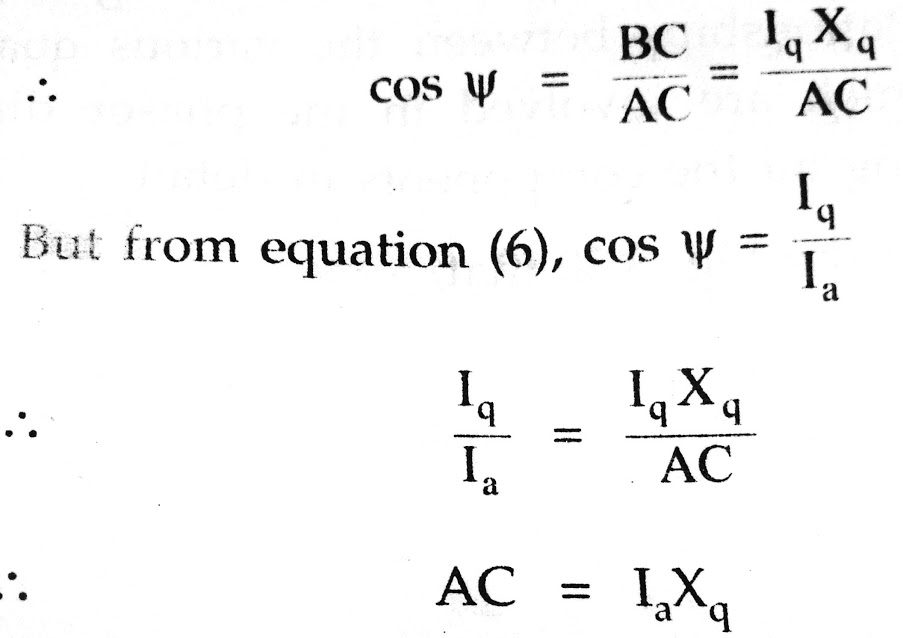
Tho point C can be located.Hence the direction of Ef is also known.Now triangle ODC is also right angle triangle,
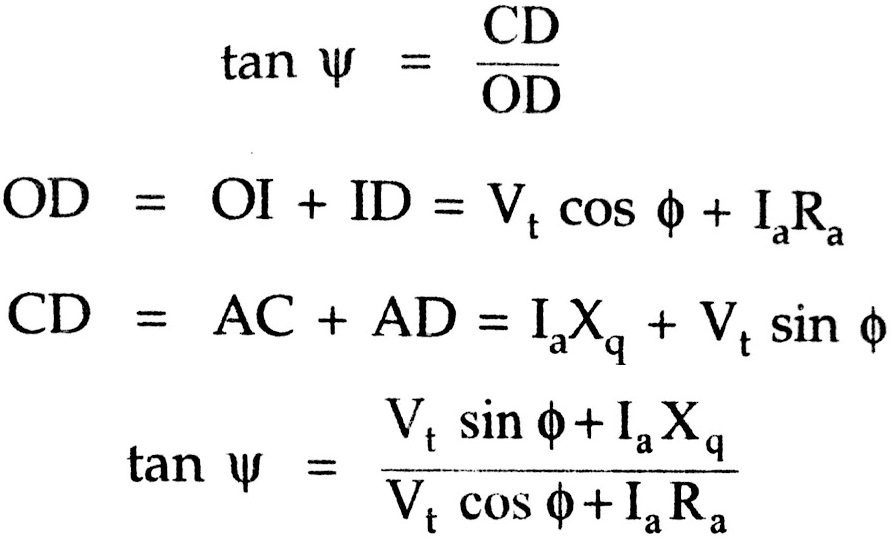
As IaXq is known, the angle Ψ can be calculated from the above equation. As Φ is known we can write,
𝛿 = Ψ – Φ for lagging p.f.
Ef = Vt cos 𝛿 + Ia Ra + Id Xd
Hence the magnitude of Ef can be obtained by using the above equation.
Must Read:
Conclusion:
Now today we have learnt about Blondel two reaction theory (Salient Pole Alternators Theory).You can download this article as pdf, ppt.
Comment below for any Queries.